Comparative Study of Heat Transfer and Flow Friction in Plate Heat Exchangers with CarboxyMethyl Cellulose and Sodium Alginate

Abstract

Study of Plate heat exchanger (PHE) with power law fluid is a very interesting topic now a days as there is improvement of thermal performance of heat exchanger. Power law fluids show complex flow behavior due to its rheological properties. The parameters which differ these power law fluids from Newtonian fluids are rheological properties like flow behavior index and power law index. Hence flow behavior index and power law index are the two parameters which affect the heat transfer rate. Now to enhance rate of heat transfer we should know how Nusselt number changes with change in flow behavior index and power law index. Hence the aim of present study was to observe how Nusselt number and friction factor changes with change in flow behavior index and power law index. For this purpose thermal performance of PHE have been studied with CorboxyMethyl Cellulose (CMC) and sodium alginate as a cold fluids. Comparison of Nusselt number and friction factor of CMC and sodium alginate have been done. It was observed that Nusselt number for CMC solution was more compared to sodium alginate solution with less friction factor than sodium alginate.

Introduction

I. INTRODUCTION

Power law fluids have attracted wide attention of the researchers in the last few decades. And study of power law fluids with Plate Heat Exchanger is the very interesting area for food industries as generally all the food fluids behave as a shear thinning power law fluids. Heat transfer processing of viscous non-Newtonian fluids is encountered in various industrial sectors including chemicals, petrochemicals, polymers, and pharmaceuticals. Comperehensive literature reviews on nonNewtonian fluid flow and heat transfer have been published by Skelland [1], Metzner [2], Lawal and Mujumdar [3], and Etemad [4]. Yoo [5] measured heat tarnsfer of nonNewtonian turbulent flow through circular tube with constant heat flux boundary condition. Joshi and Bergles [6] and Scirocco et al. [7] did an experimental investigation related the to laminar flow of pseudoplastic solutions in a circular tube subjected to a uniform wall heat flux. The results of Scirocco et al. [7] cover the turbulent regime as well.  

Literature is also available on thermal performance of PHE with power law fluid. Carla et al. (2008) presented numerically study on laminar flows of Newtonian and power-law fluids through cross-corrugated chevron type plate heat exchangers (PHEs) in terms of the geometry of the channels. Warnakulasuriya et al. (2007) [8] investigated heat transfer and pressure drop characteristics of an absorbent salt solution in a commercial plate heat exchanger serving as a solution sub-cooler in the high loop of triple-effect absorption refrigeration cycle. Established the correlation equations to predict the heat transfer and pressure drop and to analyze and optimize the operating parameters for use in the design of absorption systems. Cabral et al. (2010) [9]have studied the pressure drop of pineapple juice in a PHE with 50º chevron plates. The pressure drop of pineapple juice flowing through a PHE with 50º chevron plates was determined for various flow rates (13–119 kg/s,) and temperatures (28–81ºC). Afonso et al. (2003) [10] conducted an experimental investigation to obtain a correlation for the determination of convective heat transfer coefficient in a PHE using yogurt as test fluid [11]. Based on the experimental studies of Afonso et al. (2003)[12], Fernandes et al.[13] (2005,2006, 2007 &2008) has demonstrated numerical studies on PHE with   yogurt as test fluid. Carezzato et a.l (2007) [14] has also investigated the non-Newtonian heat transfer on a PHE with a generalized   configuration, using CMC as a test solution [15]. Similar numerical studies in a PHE using egg yolk as test fluid were conducted by Jorge et al. (2003) [16]. Renato Cabral et al. (2010) [17]studied the thermo-physical (density) and flow properties (rheology) of pineapple juice in a PHE over a considerable range of temperature and soluble solid content to obtain a correlation for the determination of friction factor versus Reynolds Number [18].

A better additive which enhances the rate of heat transfer has to be selected using the rheological parameters as the criteria for selection in order to best serve the food industry.

Hence in the present work comparative study of thermal performance of PHE have been carried out between CMC and sodium alginate as a cold fluid. Nusselt number and friction factor values of CMC, sodium alginate and water have been compared to study how shear thinning behavior affect the heat transfer. Data on Nusselt number and friction factor for CMC have been used published by Muthamizi et al. (2014)[19]. Model developed by Muthamizi et al. (2014) [19] also validated by using data experimental data in present work, and observed that it gives good results.

II. MATERIALS AND METHODS

A. Experimental Setup and Procedure

A six-channel corrugated type PHE with different flow rates and concentrations of working fluids sodium alginate was used in the present study. The apparatus shown in Fig.1consisted of a hot water storage tank,  a cold fluid storage tank , immersed type of a pair of electrical heaters, a couple of liquid Rota meters, resistance temperature detectors, a manometer, two monoblock pumps and separate collection tank for cold fluids and hot water was recycled for reuse.  A 25 liter capacity stainless steel tank for hot water storage was thermally well insulated to avoid heat loss to the atmosphere. Immersing type of electrical heaters of 4Kw capacity was fixed inside the hot water tank to raise the water temperature. A thermostat temperature controller with a range of 0°C to 110°C was connected with electrical heaters to set the temperature of hot water at a desired value.

Double pole on/off switch was connected with the 4Kw capacity electrical heaters. A monoblock type pump of 0.25 hp capacity was connected to the hot water storage tank to pump the hot water from the hot water storage tank to the PHE and a flow control valve in the same line was meant for regulating the flow. The cold fluid was stored in a separate stainless steel tank of equal capacity and well connected with another monoblock type pump of similar capacity used to pump cold fluid from cold fluid storage tank to PHE.A return flow line was provided to convey the cold fluid discharged at the outlet back into the collecting tank.

Two liquid Rotameters with an accuracy of ± 2% and measurement range of 0-10 LPM were well connected separately with the hot and the cold fluid lines to measure the fluid flow rate. These liquid flow meters were calibrated within their flow range.

Four Resistance Temperature Detectors (RTDs) of model type: PT 100 was mainly used to measure the inlet and outlet temperature of each fluid with an accuracy of ± 0.1°c. Out of the total four, two RTD’s were separately placed at the inlet ports of both the  fluids to measure the inlet fluid temperature and remaining two RTD’s were separately placed at the outlet ports of both the fluids to measure the outlet fluid temperature. Digital temperature indicators with channel selectors connected with RTD’s displayed the output results of RTDs. These RTDs were calibrated within their temperature range via the corresponding calibration procedure. Table 1 shows the specifications of PHE.

Sodium alginate pure (food grade) was provide by by LOBA Chemie, Merck & Himedia. For a constant hot fluid mass flow rate and concentration, experimental data were collected for different flow rates of sodium alginate solution (0.016-0.099 kg/s). Likewise, all runs were carried out for different concentrations (0.1-0.6%w/w) and different hot fluid mass flow rates (0.016-0.099 kg/s) as detailed in the experimental plan shown in Fig. 2.

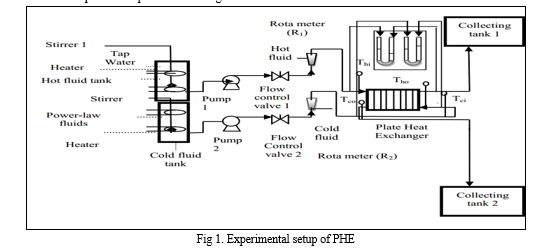
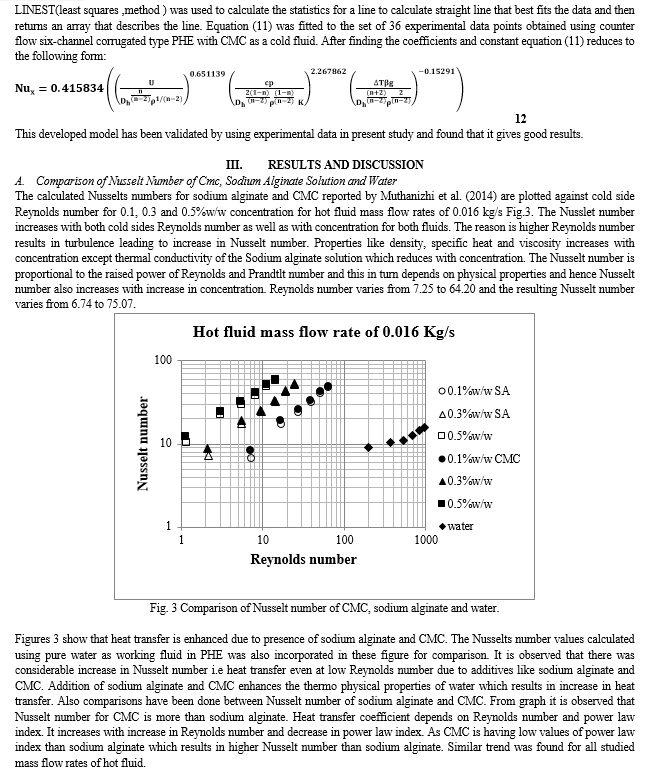
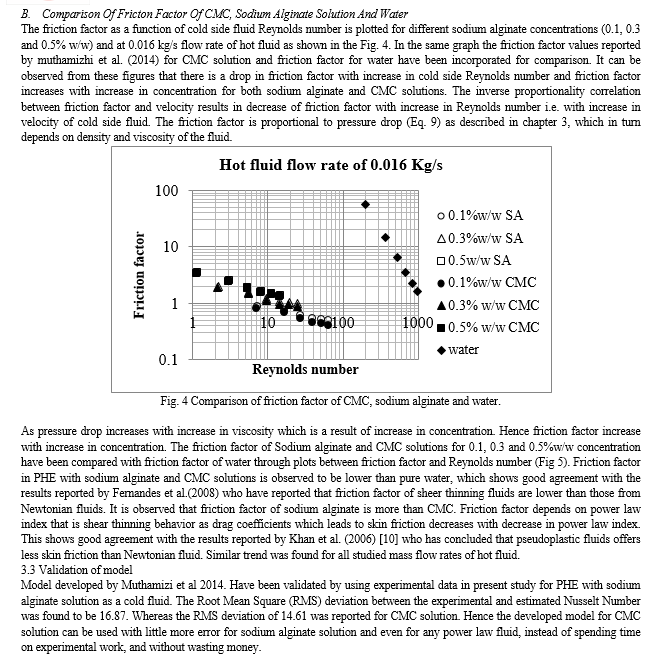
Table 1. Specifications of PHE

Fig 2. Experimental plan

1. Data Processing

The heat load, Q, of a PHE, can be represented by Eqs. 1(a, b and c).

Qh=mhCph Th, i-Th,o                                                                                                           1 (a)                                                                                 

Qc=mcCpc Tc,o-Tc,i                                                                                                             1 (b)                                                                                                                                             

Q=ApUexp?TlmFT                                                                                                                                     1 (c)              

?Tlm=Th,i-Tc,o-Th,o-Tc,ilnTh,i-Tc,oTh,o-Tc,i                                                                                                                           1 (d)

where, m mass flow rate and Cp is specific heat of fluids, A is the effective PHE area calculated by multiplying area of one plate (length x width) by no. of plates for effective heat transfer (5), Uexp is the overall heat transfer coefficient, ?Tlm is the logarithmic mean temperature difference and FT is the correction factor [18]. All quantities were known except heat transfer rate (Q=Qh=QC), which is calculated by using Eq. 1 (a&b). Thermo physical properties of sodium alginate solution thermal conductivity, density and specific heat were taken from the first phase study. The heat transfer rate calculated from above equation was then used to calculate the overall heat transfer coefficient Uexp, where ?Tlm  was calculated by Eq. 1(d). The correction factor FT  is a function of the exchanger configuration (number of transfer units (NTU, defined in Eq. (2) and heat capacity ratio (c*, defined in Eq. (3)). For pure countercurrent flow ideal case, FT =1. For all other types of flow distribution, 0<FT<1

NTU=Nc-1ApUexpminmhCph,mcCpc                                                                                                                         2                                                                                                                                                                    

C*=max mhCph,mcCpcminmhCph,mcCpc                                                                                                             3                                                                                                                                                                                

For the most usual configurations, researchers have utilized PHE simulation models to generate charts and tables in the form FT= FT (NTU, c*) or ε = ε (NTU, c*), where ε is the thermal effectiveness of the exchanger [19].       Harika et al. has developed an effectiveness chart for 9 channels corrugated counter flow heat exchanger. [20]                 

ε=QminmhCph,mCpcTh,i-Tc,i                                                                                                                     4 (a)                                            

FT =1NTU1-C* ln1-C*ε1-ε if c*<1εNTU-(1-ε) if  c*>1                                                                                       4 (b)            

After the determination of Uexp, Eq. 5 was used to calculate cold side heat transfer coefficient. In which the convective coefficient of the water side hhot of the PHE was obtained using Eq. 5, and same flow analysis as described by Vlasogiannis et al. (2002) [21]. Introducing pure water as the cold fluid and hot fluid as well, (hh=hc) the exchanger was first tested in a single-phase operation. To extract an accurate correlation for the hot fluid side heat transfer coefficient of the available PHE, a series of measurements were analyzed by the variant of the modified Wilson plot technique.

1Uexp=1hh+1hc+?xkss                                                                                                                                                        5                                          

Calculated hh was again substituted in Eq. 5 to predict cold side heat transfer coefficient (hc) where Δx is the plate thickness and kss is the thermal conductivity of the plate material (Stainless steel) [22].

Nusselt number is then calculated from Eq. 6

                                                                                                                                                   6

The pressure drop was calculated using Eq. (7) with the measured difference in the level of manometer fluid.

?p=ρgh                                                                                                                                                             7

Reynolds analogy is based on similarities between heat transfer and fluid friction (which causes the pressure drop). The simple analogy is valid only for fluids with Prandtl number equal to one. The Prandtl number expresses the relative magnitude of diffusion of momentum and heat in the fluid and thus the heat and momentum are transported at the same rate. This is not applicable to plate heat exchangers as the flow is generally turbulent with random transportation of heat and momentum. Hence the modified Reynolds analogy Colburn factor (j), which gives an approximate rationalization over a wide range of Prandlt numbers as given in Eq. (8) has been used for our calculation.

Conclusion

In this work comparison has been done between two power law fluids to select better additive. Is was found that Nusselt number increases with decrease in power law index, it shows heat augmentation is more for fluids which shows more shear thinning behaviour. Another benefit of these shear thinning power law fluids is they provide less friction than Newtonian fluids, also friction decreases with more shear thinning behaviour. Shear thinning behaviour increases with decreases in power law index. So for better heat transfer we can chose the power law fluid with law power law index.

References

[1] Skelland, A.H.P., \"Non-Newtonian flow and heat transfer\", John Wiley & Sons, (1967). [2] Metzner, A.B., Vaughn, R.D., Houghton, G.L., \"Heat transfer to non-Newtonian fluids\", AIChE Journal, 3, 92(1957). [3] Lawal, A., Mujumdar, A.S., \"Laminar duct flow and heat transfer to purely viscous nonNewtonian fluids\", in: A.S. Mujumdar, R.A. Mashelkar (eds), Advances in transport processes, Wiley Eastern, New Dehli, 352 (1989). [4] Etemad, S.GH., \"Forced convective heat transfer of non-Newtonian fluids in tubes\", Esteghlal, 1, 1 (1998). [5] Yoo, S.S., \"Heat transfer and friction factors for non-Newtonian fluids in turbulent pipe flow\", Ph.D. thesis, University of Illinois, Chicago, IL (1974). [6] Joshi, S.D., Bergles, A.E., \"Experimental study of laminar heat transfer to in-tube flow of non-Newtonian fluids\", Journal of Heat Transfer, 102, 397 (1980). [7] Sciroco, V., Devienne, R., Lebouche, M., \"Laminar and turbulent flow of a pseudoplastic fluid in a circular conduit: heat transfer coefficients\", International Chemical Engineering, 31(3), 450 (1991). [8] Fernandes, Carla S., et al. \"Laminar flow in chevron-type plate heat exchangers: CFD analysis of tortuosity, shape factor and friction factor.\" Chemical Engineering and Processing: Process Intensification 46.9 (2007): 825-833. [9] Carla S. Fernandes, Ricardo P. Dias, João M. Nóbrega, João M. Maia, Friction factors of power-law fluids in chevron-type plate heat exchangers. “Journal of Food Engineering” 89.5 (/2008);441-447. [10] Warnakulasuriya, F. S. K., and W. M. Worek. \"Heat transfer and pressure drop properties of high viscous solutions in plate heat exchangers.\" International Journal of Heat and Mass Transfer 51.1 (2008): 52-67. [11] Galiullina, G. R., E. K. Vachagina, and G. R. Khalitova. \"Heat transfer of non-Newtonian liquid flows in convergent-divergent channels with fourth-kind thermal boundary conditions.\" Thermophysics and Aeromechanics 17.1 (2010): 83-89. [12] Moradi, M., S. Gh Etemad, and A. Moheb. \"Laminar flow heat transfer of a pseudoplastic fluid through a double pipe heat exchanger.\" Iranian Journal of Chemical Engineering 3.2 (2006): 13-19. [13] R. A. F. Cabral, J. A. W. Gut, V. R. N. Telis, J. Telis-Romero, Non-newtonian flow and pressure drop of pineapple juice in a plate heat exchanger, “Brazilian Journal of Chemical Engineering”27.4 (2010). [14] Scariot, M. R., M. I. Berto, and V. Silveira. \"Simulation of The Temperature Profile of a Pectin Solution in a Plate Heat Exchanger: a Non-Linear System Approach for Control.\" Revista de Engenharia Térmica 4.1 (2005). [15] Carezzato, Alessandra, et al. \"Non?Newtonian Heat Transfer on a Plate Heat Exchanger with Generalized Configurations.\" Chemical engineering & technology 30.1 (2007): 21-26. [16] M. Moradi, S. Gh. Etemad, and A. Moheb, Laminar Flow Heat Transfer of a Pseudoplastic Fluid through a Double Pipe Heat Exchanger, “Iranian Journal of Chemical Engineering”, 2.3 (2006) [17] W. A. Khan, J. R. Culham and M. M. Yovanovich, Fluid Flow and Heat Transfer in Power-Law Fluids Across Circular Cylinders: Analytical Study, “J. Heat Transfer”,128.9, (2006), 870-878. [18] Jorge A.W. Gut, Renato Fernandes, Jose M. Pinto, Carmen C. Tadinia (2004) Thermal model validation of Plate Heat Exchnagers with generalized configurations, Chemical Engineering Science. 59: 4591– 4600. [19] Harika Sammeta, Kalaichelvi Ponnusamy, M.A. Majid, K. Dheenathayalan, Effectiveness charts for counter flow corrugated plate heat exchanger, “Simulation Modelling Practice and Theory” 19 (2011) 777–784. [20] Vlasogiannis P, Karagiannis G, Argyropoulos P, Bontozoglou V (2002) Air–water two-phase flow and heat transfer in a Plate Heat Exchanger, International Journal of Multiphase Flow. 28: 757–772. [21] Muthamizhi .K and Kalaichelvi .P, Development of Nusselt number correlation using dimensional analysis for Plate heat exchanger with a Carboxymethyl cellulose solution, “Heat and Mass Transfer”. [22] Manjula P, Kalaichelvi P and Dheenathayalan K (2009) Development of mixing time correlation for a double jet mixer, Wiley Interscience.8. [23] Moradi M, Etemad S Gh, and Moheb A, (2006) Laminar Flow Heat Transfer of a Pseudoplastic Fluid through a Double Pipe Heat Exchanger, Vol. 3, No. 2 (Spring), IAChE, Department of Chemical Engineering, Isfahan University of Technology, Isfahan, Iran. [24] Fernandes CS, Dias RP, Nobrega JM (2008) Maia Friction factors of power-law fluids in chevron-type Plate Heat Exchangers, Journal of Food Engineering. 89:441–447. [25] Fernandes CS, Dias RP, Nobrega JM, Afonso IM, Melo LF, J.M. Maia (2005) Simulation of stirred yoghurt processing in Plate Heat Exchangers, Journal of Food Engineering. 69: 281–290. [26] Afonso IM, Maia L, Melo LF (2003) Heat transfer and rheology of stirred yoghurt during cooling in Plate Heat Exchangers, Journal of Food Engineering. 57:179–187. [27] Edwards MF, Changal Vaie AA and Parrott DL, (1974) Heat Transfer and Pressure Drop Characteristics of a Plate Heat Exchanger Using Newtonian and Non-Newtonian Liquids, The Chemical Engineer. 286-288. [28] Shah RK, Focke WW, (1988) Plate Heat Exchangers and their design theory. In: Shah RK, Subbarao EC, Mashelkar RA. (Eds.), Heat Transfer Equipment Design. Hemisphere, New York. [29] R.P. Bharti, P. Sivakumar, R.P. Chhabra, Forced convection heat transfer from an ellipticalcylinder to power-law ?uids, International Journal of Heat and Mass Transfer 51 (2008) 1838–1853.

Copyright

Copyright © 2024 Shubhangi S. Patil, K. Muthamizhi, P. Kalaichelvi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.